到目前为止，我们将二进制数的讨论限制为 无符号（严格非负）整数。本节介绍了包含负数的二进制的另一种解释。鉴于变量的存储空间有限，有符号二进制编码必须区分负值、零和正值。操作带符号的数字还需要一个对数字取反的过程。

有符号二进制编码必须将位序列划分为负值和非负值。在实践中，系统设计师构建 通用 系统，因此 50% / 50% 的分割是一个不错的中间选择。因此，本章介绍的有符号数编码表示相同数量的负值和非负值。

非负与正

请注意，非负 和 正 之间存在微妙但重要的区别。严格正值集合不包括零，而非负值集合包括零。即使将可用位序列在负值和非负值之间划分为 50% / 50%，非负值之一仍必须保留为零。因此，在位数固定的情况下，数字系统最终可能会表示比正值更多的负值（例如，在二进制补码(two’s complement system)系统中）。

有符号数编码使用一位来区分 负 数集和 非负 数集。按照惯例，最左边的位指示数字是负数 (1) 还是非负数 (0)。最左边的位称为高位或最高有效位。

本章介绍了两种可能的有符号二进制编码 — 有符号量值 和 二进制补码。尽管在实践中仅使用其中一种编码（二进制补码），但对它们进行比较将有助于说明它们的重要特征。

4.3.1. 有符号量值

有符号量值（signed magnitude）表示将高阶位专门视为符号位。也就是说，高位是 0 还是 1 并不影响数字的绝对值，它只决定该值是正（高位 0）还是负（高位 1）。与二进制补码相比，带符号的大小使得十进制转换和求反过程相对简单：

  • 要计算 N 位有符号量值序列的十进制值，请使用熟悉的无符号方法 计算数字 d0 到 dN-2 的值。然后，检查最高有效位dN-1：如果为1，则值为负数；否则就不是负数。
  • 要对某个值求反，只需翻转最高有效位即可更改其符号。

负值误解（negation misconception）

带符号的量值纯粹出于教学目的。尽管过去的一些机器（例如 20 世纪 60 年代的 IBM 的 7090）使用了它），但没有现代系统使用有符号大小来表示整数（尽管类似的机制 是 存储标准的一部分[浮点值](https://en.wikipedia.org/wiki/Single- precision_floating-point_format))。

除非明确要求您考虑带符号的大小，否则您不应该假设翻转二进制数的第一位会在现代系统上得到该数字的负数值。

图 1 显示四位有符号量值序列如何与十进制值相对应。乍一看，有符号量值可能因其简单性而显得很有吸引力。不幸的是，它有两个主要缺点，使其没有吸引力。第一个是它呈现了 两个 零的表示形式。例如，对于四位，带符号的量值表示 零 (0b0000) 和 负零 (0b1000)。因此，它给硬件设计者带来了挑战，因为硬件需要考虑两个可能的二进制序列，尽管它们具有不同的位值，但它们在数值上相等。只需用一种方式来表示如此重要的数字，硬件设计师的工作就会容易得多。

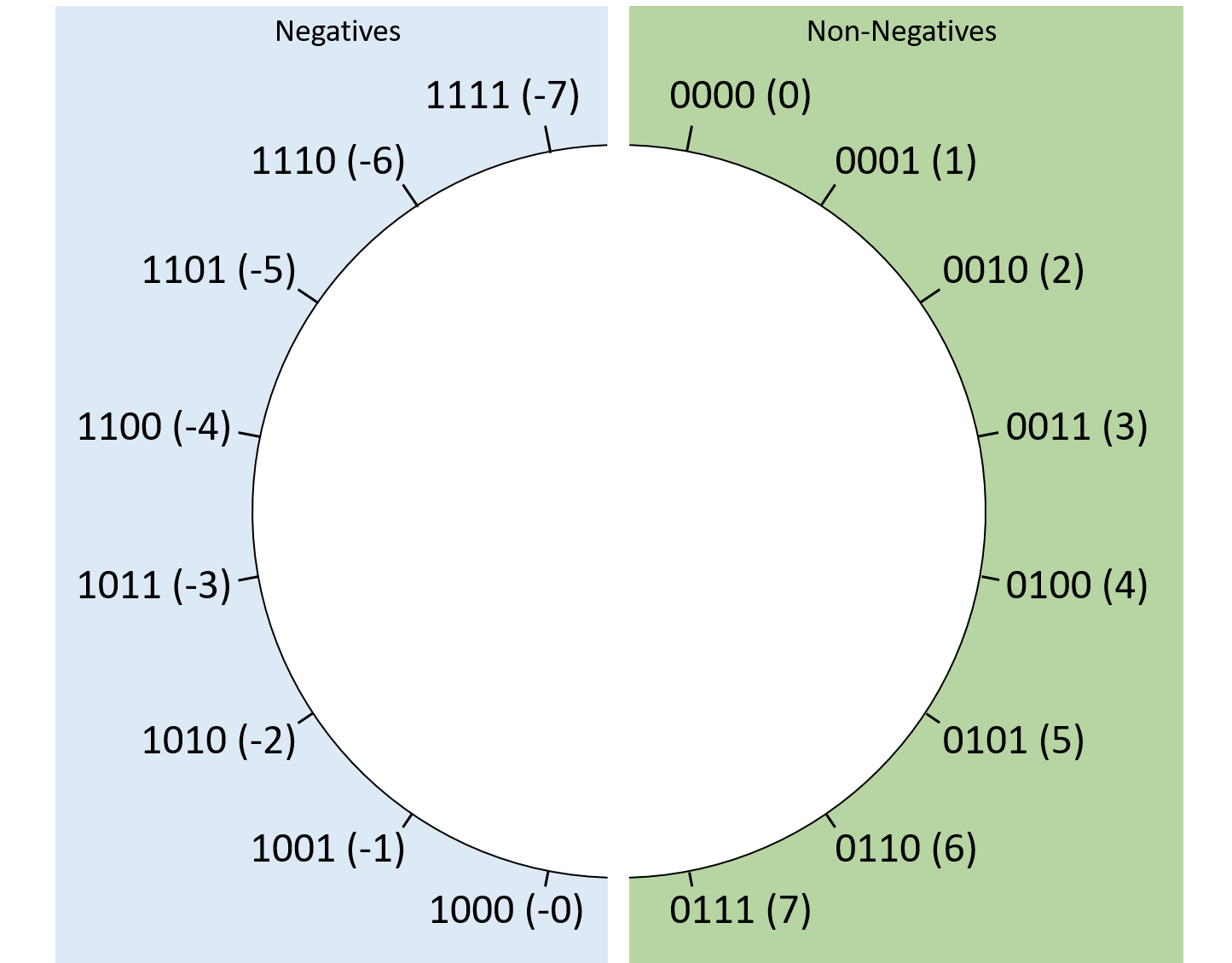A circle with non-negative values on one side ranging from 0b0000 (0) to 0b0111 (7). The other side holds 0b1000 (-0) to 0b1111 (-7). 图 1. 长度为 4 的位序列的带符号量值的逻辑布局。

有符号量值的另一个缺点是它在负值和零之间表现出不方便的不连续性。虽然我们稍后会更详细地介绍溢出，但向四位序列 0b1111 添加 1 会“翻转”回 0b0000。对于带符号的量值，此效应意味着 0b1111 (-7) + 1 可能会被误认为 0 而不是预期的 -6。这个问题是可以解决的，但该解决方案再次使硬件设计变得复杂，本质上将负整数和非负整数之间的任何转换变成需要额外小心的特殊情况。

由于这些原因，符号大小在实践中基本上消失了，而补码占据了主导地位。

4.3.2. 补码(Two’s Complement)

二进制补码编码以一种优雅的方式解决了有符号幅度的问题。与带符号的大小一样，二进制补码数的高位指示该值是否应解释为负数。但相比之下，高位也会影响数字的值。那么，如何才能做到这两点呢？

计算 N 位二进制补码的十进制值类似于熟悉的无符号方法，只不过高位对整体值的贡献被否定。也就是说，对于 N 位二进制补码序列，不是第一位为总和贡献dN-1 × 2N-1，而是贡献 -dN-1 × 2N-1 （注意负号）。因此，如果最高有效位是 1，则总值将为负，因为第一位对总和贡献的绝对值最大。否则，第一位对总和没有任何贡献，并且结果为非负数。完整的公式是：

- (dN-1 × 2N-1)    +    (dN-2 × 2N-2)    +    …​    +    (d2 × 22)    +    (d1 × 21)    +    (d0 × 20) ^ 请注意第一个项的前导负号！

图 2 展示了二进制补码形式的四位序列的布局。该定义仅编码零的一种表示形式——全为 0 的位序列。仅使用单个 zero 序列，二进制补码表示的负值比正值多一个。以四位序列为例，二进制补码表示最小值为 0b1000（-8），但最大值仅为 0b0111（7）。幸运的是，这种怪癖不会妨碍硬件设计，也很少会给应用程序带来问题。

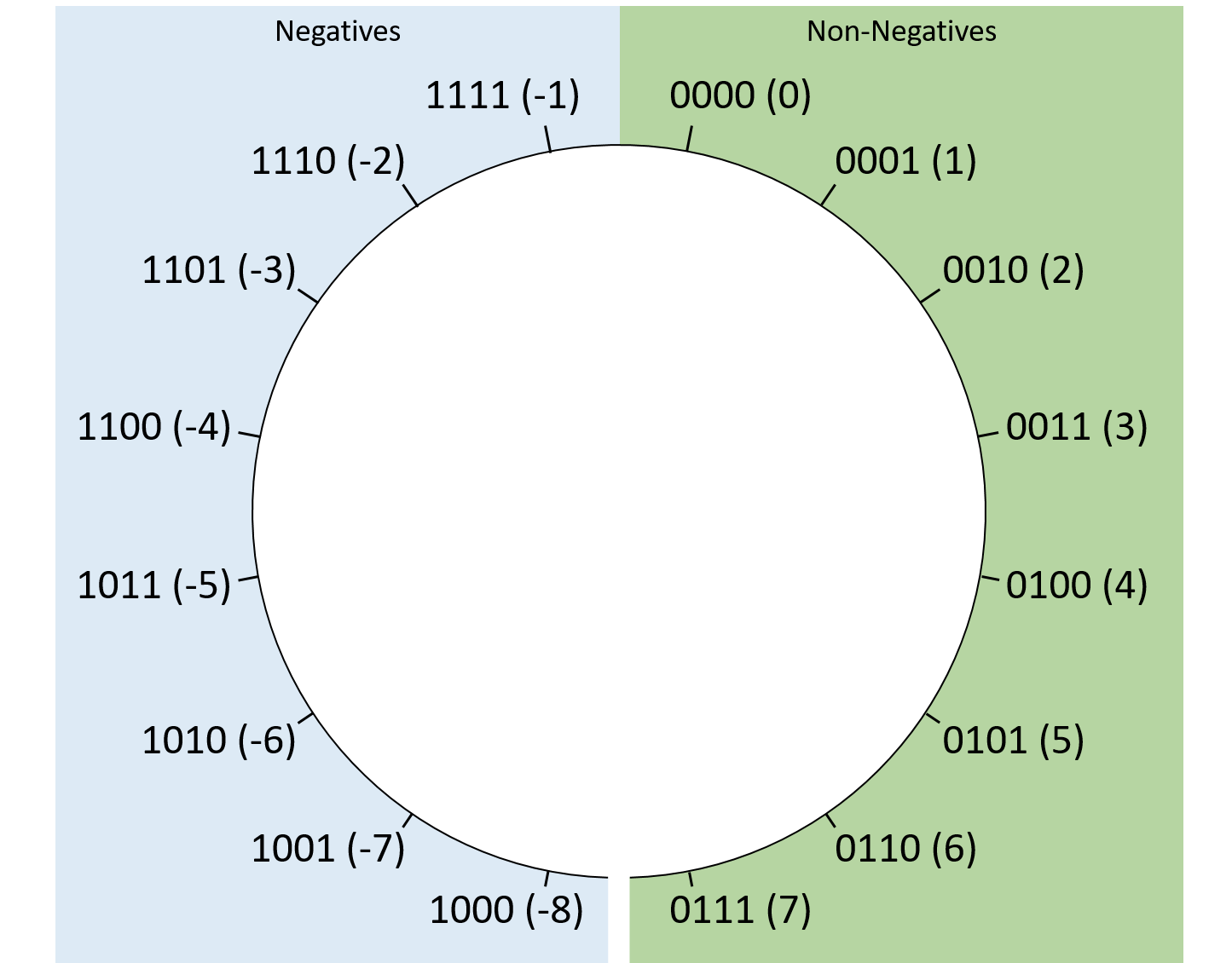A circle with non-negative values on one side ranging from 0b0000 (0) to 0b0111 (7). The other side holds 0b1111 (-1) to 0b1000 (-8). 图 2. 长度为 4 的位序列的二进制补码值的逻辑布局。

与有符号的大小相比，二进制补码还简化了负数和零之间的转换。无论用于存储它的位数有多少，由全 1 组成的二进制补码数将始终保持值 -1。将 1 添加到全 1 的位序列“翻转”为零，这使得补码变得很方便，因为 -1 + 1 应该 产生零。

负值与取反

对二进制补码取反比对带符号的数值取反要稍微棘手一些。要否定 N 位值，请确定其相对于 2N 的补码（这就是编码名称的来源）。换句话说，要对 N 位值 X 求反，请找到一个位序列 Y（X 的补码），使得 X + Y = 2N。

Fortunately, there’s a quick shortcut for negating a two’s complement number in practice: flip all the bits and add one. For example, to negate the eight-bit value 13, first determine the binary value of 13. Because 13 is the sum of 8, 4, and 1, set the bits in positions 3, 2, and 0: 幸运的是，在实践中，有一个快速的捷径可以对二进制补码求反：翻转所有位并加一。例如，要对八位值 13 求反，首先确定 13 的二进制值。因为 13 是 8、4 和 1 的和，所以将位设置在位置 3、2 和 0：

00001101  (decimal 13)

接下来，“翻转位”（将所有零更改为一，反之亦然）：

11110010

最后，加 1 得到 0b11110011。果然，应用解释二进制补码位序列的公式显示该值为 -13：

-(1 × 27)    +    (1 × 26)    +    (1 × 25)    +    (1 × 24)    +    (0 × 23)    +    (0 × 22)    +    (1 × 21)    +    (1 × 20)

  =    -128 + 64 + 32 + 16 + 0 + 0 + 2 + 1    =    -13

如果您好奇为什么这个看似神奇的捷径有效，请更正式地考虑 13 的八位求反。要找到 13 的补码，请求解 0b00001101 (13) + Y = 0b100000000（28，需要额外的位来表示）。该方程可以重新排列为 Y = 0b100000000 - 0b00001101。这显然是一个减法问题：

 100000000  (256)
- 00001101   (13)

虽然这样的减法可能看起来令人畏惧，但我们可以用一种更容易计算的方式将其表示为 (0b011111111 + 1) - 0b00001101。请注意，此更改只是将 28 (256) 表示为 (255 + 1)。更改后，算术如下所示：

 011111111  (255)  + 00000001  (1)
- 00001101   (13)

事实证明，对于任何位值 b，1 - b 相当于“翻转”该位。因此，前面示例中的整个减法可以简化为仅翻转较低数字的所有位。剩下的就是将 256 表示为 255 + 1 时剩下的 +1 相加。将它们放在一起，我们可以简单地翻转一个值的位并加 1 来计算其补码！

c programming with signed versus unsigned integers

除了分配空间之外，在 C 中声明变量还可以告诉编译器您希望如何解释该变量。当您声明int时，编译器会将该变量解释为带符号的二进制补码整数。要分配无符号值，请声明unsigned int。

 这种区别在其他地方也与 C 相关，例如 printf 函数。正如本章自始至终强调的那样，一个位序列可以用不同的方式解释！对于 printf，解释取决于您使用的格式占位符。例如：  

#include <stdio.h>

int main(void) {

int example = -100;

/* Print example int using both signed and unsigned placeholders. */ >printf("%d %u\n", example, example);

return 0; }

 
 即使此代码将同一变量（`example`）传递给`printf`两次，它也会打印`-100 4294967196`。小心正确地解释变量的值！

符号位扩展

有时，您可能会发现自己想要对使用不同位数存储的两个数字执行算术运算。例如，在 C 中，您可能想要添加一个 32 位int和一个 16 位short。在这种情况下，较小的数字需要符号扩展，这是一种奇特的说法，它的最高有效位根据需要重复多次，以将位序列的长度扩展到目标长度。尽管编译器会在 C 语言中为您处理这些位，但了解该过程的工作原理仍然很有帮助。

例如，要将四位序列 0b0110 (6) 扩展为八位序列，请采用高位 (0) 并将其添加到前面四次以生成扩展值：0b00000110（仍然是 6）。将 0b1011 (-5) 扩展为八位序列类似地采用高位（这次是 1）并将其四次添加到结果扩展值：0b11111011（仍然是 -5）。要验证正确性，请考虑添加每个新位后值如何变化：

    0b1011 =                       -8 + 0 + 2 + 1  =  -5
   0b11011 =                  -16 + 8 + 0 + 2 + 1  =  -5
  0b111011 =             -32 + 16 + 8 + 0 + 2 + 1  =  -5
 0b1111011 =        -64 + 32 + 16 + 8 + 0 + 2 + 1  =  -5
0b11111011 =  -128 + 64 + 32 + 16 + 8 + 0 + 2 + 1  =  -5

正如示例所证明的，非负数（高位零）在前面添加零后仍保持非负数。同样，负数（1 的高位）在将其添加到扩展值之后仍然为负数。

无符号零扩展(unsigned zero extension)

对于无符号值（例如，使用无符号限定符显式声明的 C 变量），将其扩展为更长的位序列需要零扩展，因为无符号限定符可防止该值被解释为负数。零扩展只是将零前置到扩展位序列的高位位。例如，0b1110（当解释为无符号时为 14！）扩展为 0b00001110，尽管最初的前导是 1。